西瓜书6 支持向量机
函数间隔与几何间隔
支持向量机是一种经典的二分类模型
分类学习的基本思想就是基于训练集在样本空间找到一个划分超平面,将不同类别的样本分开,但是能将样本分开的有很多我们应该找那个最中间的超平面,因为其容忍度最好。如下图所示应该用最中间的红色面
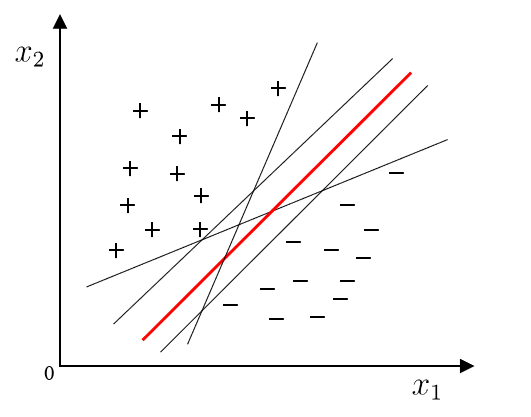
当超平面距离与它最近的数据点的间隔越大,分类的鲁棒性越好,即当新的数据点加入时,超平面对这些点的适应性最强,出错的可能性最小。
因此需要让所选择的超平面能够最大化这个间隔 Gap, 常用的间隔定义有两种,一种称之为函数间隔,一种为几何间隔。
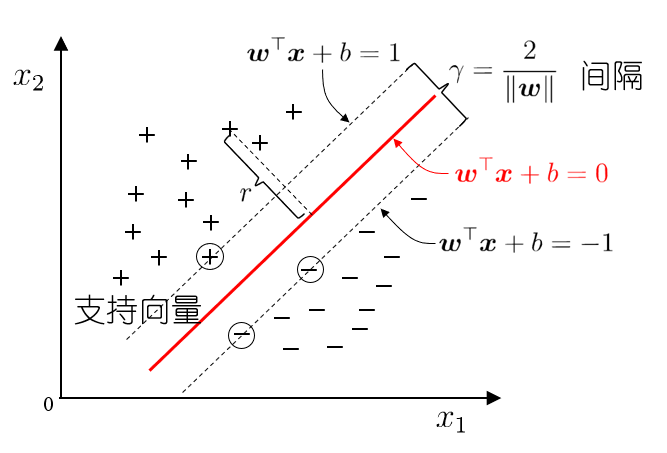
首先超平面分为线性的和非线性的,线性的一般来说就是SVM法来分类,非线性的就是用核方法来映射到高维空间使之有线性的性质。简要介绍一下超平面的一些性质:
- 法向量恒垂直于超平面。
- 和法向量相同的点代入超平面方程恒大于零,否则恒小于等于零(下面计算间隔距离时候的假设可以看出)
- 法向量和位移项确定唯一一个超平面
- 等倍缩放法向量和偏移值超平面不变
函数间隔
在SVM中,我们用一个超平面
定义:
函数间隔
简单来说,函数间隔是超平面输出
含义:
如果
如果
乘上标签
对于整个训练数据集
这个最小值反映了超平面分类能力的最“短板”——离超平面最近的点决定了整体的安全性。
几何间隔
函数间隔的问题:它会受到超平面参数
举个例子:假设有个超平面
超平面本身没变(两边还是相等的,分割效果一样)。但函数间隔
因为函数间隔有这个缺陷,我们需要一个更靠谱的指标来衡量点到超平面的真实距离。这就引出了几何间隔(geometrical margin)。
样本空间中任意一点
其中
最大间隔与支持向量
间隔(margin)是指两个边界超平面(
支持向量(support vectors)是指那些恰好位于边界上的样本点,即满足
为了最大化间隔,SVM的数学优化问题可以表示为:
s.t.
其中:
约束条件
为了计算方便,将最大化
s.t.
取
对偶问题

核函数
非线性数据(非线性问题——>线性问题)
原理是将数据映射到高维数据,在高维空间线性可分。
从低维转换到高维,
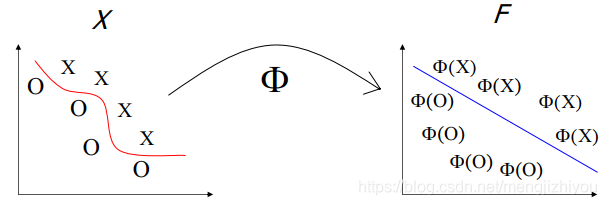
高维的特征空间的特征向量设为

我们把上面的内积表示成:
那么什么样的函数可以作为核函数呢?我们有Mercer定理 (充分非必要):只要一个对称函数所对应的核矩阵半正定, 则它就能作为核函数来使用. 核矩阵和常用的核函数如下图所示:


软间隔支持向量机
现实中, 很难确定合适的核函数使得训练样本在特征空间中线性可分; 同时一个线性可分的结果也很难断定是否是有过拟合造成的,所以引入”软间隔”的概念, 允许支持向量机在一些样本上不满足约束.
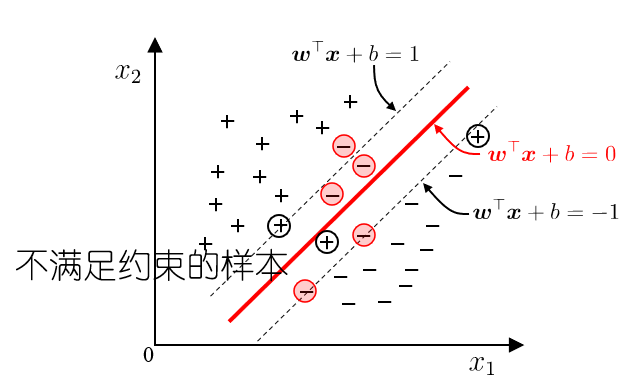
这样优化目标变为:
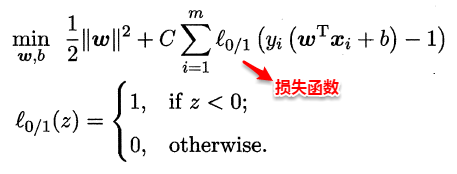
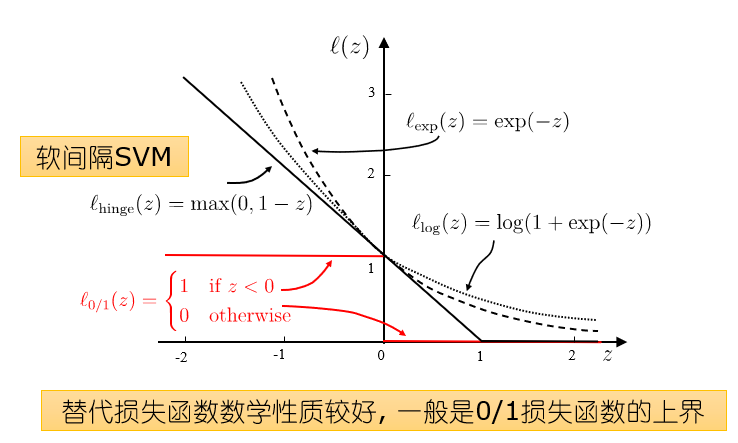
如同阶跃函数,0/1 损失函数虽然表示效果最好,但是数学性质不佳。因此常用其它函数作为“替代损失函数”。